9.32
Previous experience shows the variance of a given process to be 14. Researchers are testing to determine whether this value has changed. They gather the following dozen measurements of the process. Use these data and α = .05 to test the null hypothesis about the variance. Assume the measurements are normally distributed.
|
52 |
44 |
51 |
58 |
48 |
49 |
|
38 |
49 |
50 |
42 |
55 |
51 |
n = 12
α = .05
σ2 = 14
s2 = ?
![]()
Step #1: Hypothesize.
H0: σ2 = 14
Ha: σ2 ≠ 14
This is a two-tailed test.
Step #2: Test.
Data is assumed to be normally distributed.
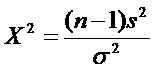
Step #3:
α = .05, α/2 = .025
Step #4:
df = n -1
df = 12 -1 = 11
The two critical chi-square values are: ![]() and
and ![]()
From Table A.8:
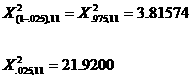
Now calculate the chi-square value. IF the calculated (observed) chi-square value is:
3.81574 < ![]() <
21.9200
<
21.9200
we will FAIL to reject the null hypothesis.
Step #6:
From excel calculations:
s2 = 30.08
The observed chi-square value is calculated as:
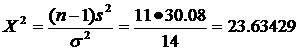
Step #7: Action.
This observed chi-square value is in the Rejection Region because:
![]()
The company REJECTS the null hypothesis.
The results indication, with 95% confidence, that the variance is not 14.
